L0-Sampler: An L0 Model Guided Volume Sampling for NeRF

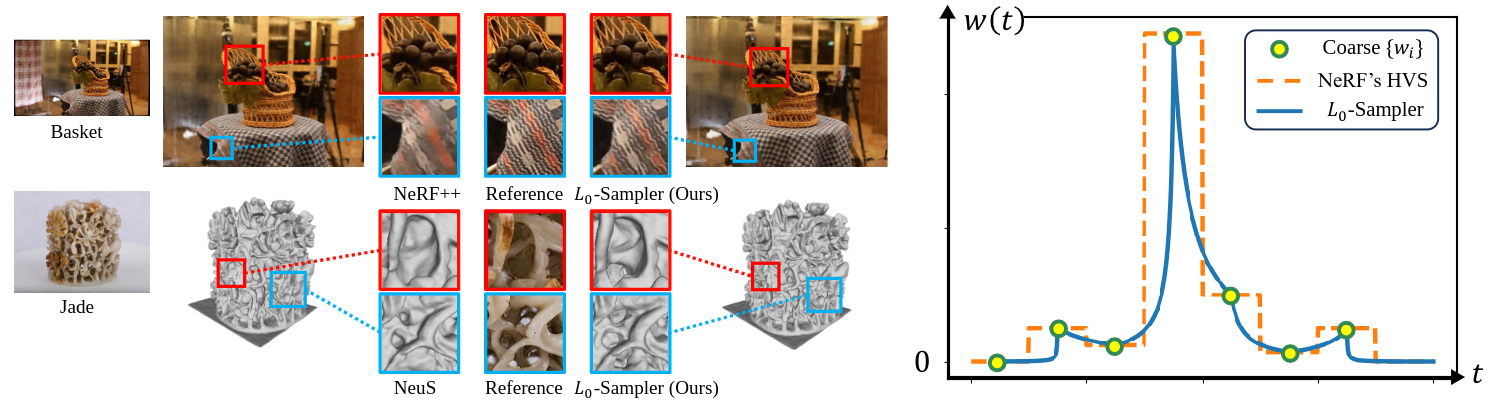
Since being proposed, Neural Radiance Fields (NeRF) have achieved great success in related tasks, mainly adopting the hierarchical volume sampling (HVS) strategy for volume rendering. However, NeRF's HVS approximates distributions using piecewise constant functions, which provides a relatively rough estimation.

Based on the observation that a well-trained weight function w(t) and the L0 distance between points and the surface have very high similarity, we propose L0-Sampler by incorporating the L0 model into w(t) to guide the sampling process. Specifically, we propose to use piecewise exponential functions rather than piecewise constant functions for interpolation, which can not only approximate quasi-L0 weight distributions along rays quite well but also can be easily implemented with few lines of code without additional computational burden. Stable performance improvements can be achieved by applying L0-Sampler to NeRF and its related tasks like 3D reconstruction.

During volume rendering, the color weight function w(t), exhibits a unique property known as the "L0 property": In scenes where a surface S is present, most points in space have a density of 0, except for the surface points. Consequently, the weight of points along the ray takes on a similar form to the L0 distance between the points and the surface. To incorporate the L0 property into the weight function, we employ a method of interpolation. In this way, we obtain a quasi-L0 function that balances the optimization of the residual space while preserving the L0 property to a certain degree.

The figure above is an overview of our L0-Sampler pipeline. The red dash line represents the surface. During hierarchical volume sampling, we first uniformly sample some points as NeRF in the coarse stage, and then through piecewise interpolation, we fit a quasi-L0 w(t) resembling an indicator function, which is in line with the L0 distance between points and surface. After normalization, it can be used as a PDF to guide inverse transform sampling. The sampling frequency in each interval (right) shows that our method can make the sampling more focused near the surface.

Only a few lines of changes were needed in key sections of code to convert NeRF's HVS into ours. For complete code please click HERE.

def sample_pdf(bins, weights, N_samples, det=False, pytest=False):
    # Maxblur
  
+   weights_pad = torch.cat([weights[..., :1], weights, weights[..., -1:]], axis=-1)
+   weights_max = torch.maximum(weights_pad[..., :-1], weights_pad[..., 1:])
+   weights = 0.5 * (weights_max[..., :-1] + weights_max[..., 1:])
  
    weights = weights + 1e-5 # prevent nans
          
    #Get integral
+   integral = (weights[..., 1:] - weights[..., :-1])/(torch.log(weights[..., 1:]/weights[..., :-1]) + 1e-6)
          
    # Get pdf
    pdf = integral / torch.sum(integral, -1, keepdim=True) # Here NeRF uses weights to normalize
    cdf = torch.cumsum(pdf, -1)
    cdf = torch.cat([torch.zeros_like(cdf[...,:1]), cdf], -1)
                        .
                        .
                        .
    matched_shape = [inds_g.shape[0], inds_g.shape[1], cdf.shape[-1]]
    cdf_g = torch.gather(cdf.unsqueeze(1).expand(matched_shape), 2, inds_g)
    bins_g = torch.gather(bins.unsqueeze(1).expand(matched_shape), 2, inds_g)
          
-   denom = (cdf_g[...,1]-cdf_g[...,0])
-   denom = torch.where(denom < 1e-5, torch.ones_like(denom), denom)
-   t = (u-cdf_g[...,0])/denom
          
    # Find Roots
+   residual = u-cdf_g[...,0]
+   rhs = residual * torch.sum(integral, dim = -1, keepdim = True)
+   weights_g = torch.gather(weights.unsqueeze(1).expand(matched_shape), 2, inds_g)
+   denom = torch.log(weights_g[..., 1]/weights_g[..., 0]) + 1e-6
+   t = torch.log1p(rhs*denom/weights_g[..., 0]) / denom
          
  samples = bins_g[...,0] + t * (bins_g[...,1]-bins_g[...,0])
          
  return samples
            

Here are the rendering results of NeRF and NeRF w/ our L0-Sampler on the Lego dataset. Use the slider here to see the differences between them in detail.